Previously, we’ve looked at the pivot table summary functions: Count, Average, Min and Max and Product. In this article we’ll look at the StdDev and StdDevp summary functions.
StdDev Function and StdDevp Function
Like the STDEV.P and STDEV.S worksheet functions, the StdDev and StdDevp summary functions calculate the standard deviation for the underlying data in the Values area, and is the square root of the variance. Like the variance, standard deviation is a measure of how widely the values vary from the average of the values.
The StdDevp summary function is used when the entire population is used in the calculation. If a sample of the data is used, instead of the entire population, then use the StdDev summary function.
STDEV.P Worksheet Function
Shown below is the pivot table source data, and the STDEV.P worksheet function is calculating the standard deviation for each product type. There is a large difference between the quantities of file folders sold, and the standard deviation is 44.5. For the paper sales, the difference in quantity is much smaller, and the standard deviation is only 4.71.
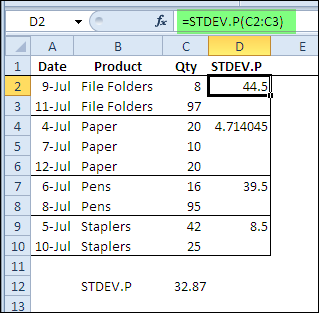
Pivot Table StdDevp Summary Function
To use the StdDevp summary function, when the Qty field is added to the pivot table, change the summary calculation to StdDevp.
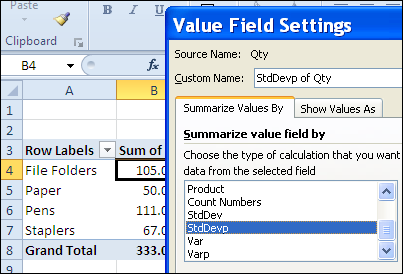
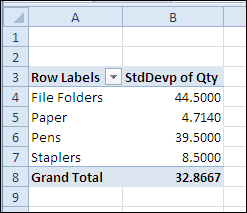
The standard deviations shown in the pivot table are the same as those that were calculated on the worksheet.
Note: If the count of items is one, a #DIV/0! error is displayed when using the StdDev summary function, because one is subtracted from the count when calculating the standard deviation.
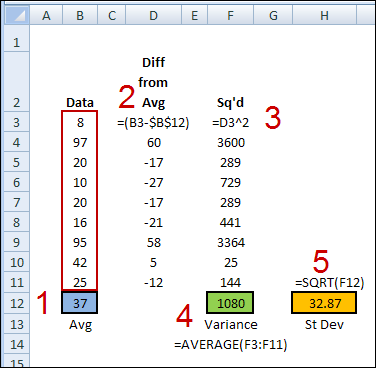
How the Standard Deviation is calculated
In the standard deviation, each number is compared to the mean of the numbers. If you were to calculate the standard deviation on the worksheet, without the STDEV.P function, here’s how you would do it.
- Find the average of the numbers in the pivot table data.
- From each number, subtract the average.
- Square the calculated difference for each number
- Find the average of the squared difference.
- Find the square root of the average.
_______________

should the standard deviation not be between 0 to 1?
that would be the relative standard deviation.
for that you divide the standard deviation throug the average